Selve opgaveløsningen - klassiske beregningsopgaver

Naturligvis er opgavens type ret afgørende for, hvordan den optimale løsning ser ud. Alligevel er der nogle retningslinjer, der stort set altid gælder:

Der skal være en intro.

Alle udregninger (også mellemregninger) skal med, og de skal have enheder på tallene (cm, kr osv.), hvis der er nogle.

Der skal dobbeltunderstregning under opgavens endelige resultat.

Der skal formuleres en kort og præcis konklusion til sidst.

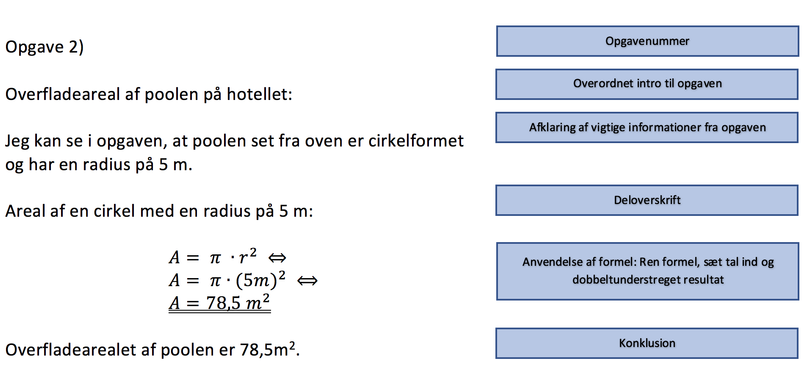
Herunder er vist et eksempel på løsning af to helt klassiske opgavetyper:

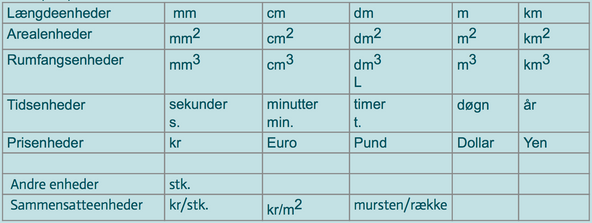
Enheder

Enheder er tallets "efternavn", når det beskriver en handling.

Eksempler på enheder:

Opgaveløsning med brug af Excel eller Geogebra

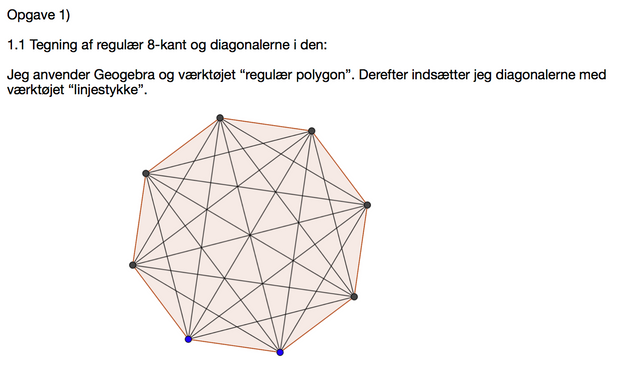
Når en opgave eksempelvis lyder:

"Tegn en regulær 8-kant og indsæt alle diagonalerne i den."

Så skal der laves en såkaldt metodebeskrivelse i opgaven, der fortæller, hvordan man har løst opgaven. Det svarer lidt til en udregning. Hvis man har anvendt Geogebra kan løsningen se således ud:

Når man så trykker "Sæt ind" eller CTRL+v så bliver billedet sat ind. I Word kan man derefter beskære billedet.

Forklaringsopgaver

Når en opgave eksempelvis lyder:

"Anne siger, at arealet af et kvadrat beregnes ved at gange de to diagonaler med hinanden. Men Theis siger, at man skal gange de to sider i kvadratet med hinanden. Afgør hvem af Anne og Theis, der har ret og begrund hvorfor."

Så skal der laves undersøgelser og begrundes grundigt. Det er ikke nok, blot at skrive et svar eller et gæt. Man viser sin undersøgelse af de to udsagn og forklarer grundigt, hvorfor man mener at Theis har ret.

Der findes mange forskellige typer af forklaringsopgaver, men fælles for dem er, at man skal vise sine beregninger og/eller undersøgelser, og ikke springe direkte til at konkludere.

Til sidst i besvarelsen af en forklaringsopgave skal der laves en kort og præcis konklusion, som man også gør i de andre opgavetyper.

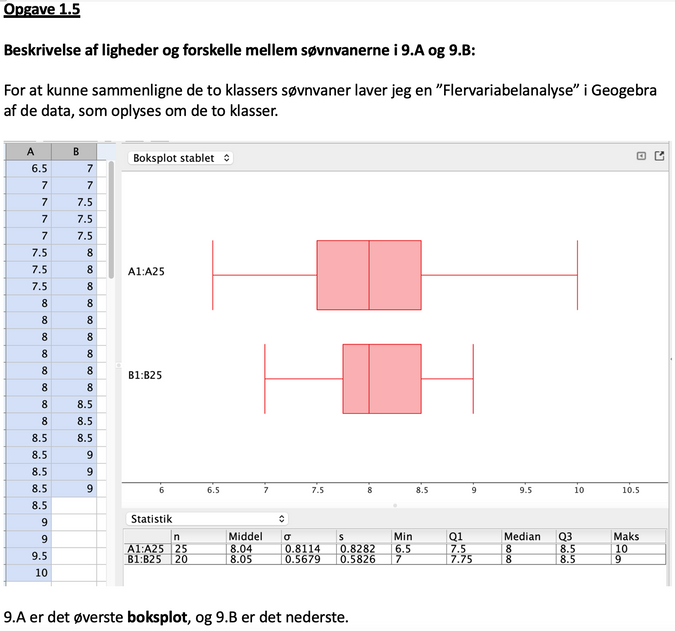
Sammenligningsopgaver - statistik

Herunder ses et eksempel på løsningen af en eksamensopgave, hvor man skal sammenligne to klassers søvnvaner. Læg mærke til, hvor mange matematiske ord, der anvedes, hvor mange konkrete tal fra min undersøgelse, samt den opsummerende konklusion, så man ikke blot siger "den ene har en størsteværdi på 10 og den anden har en på 9". Der skal lgie knyttes lidt ord til, så man bruger oplysningen til noget analyserende.

Øvelser

Opgave 1: Øvelse i at formulere introer

Nedenfor er en masse opgaver (dog mangler al den info, man har brug for for at kunne beregne noget som helst). Det eneste du skal gøre, er at formulere en intro til den opgave der er stillet. Se eksemplet først.

Eksempel

Opgave: Beregn prisen på Ivers nye bil.

Din introformulering:  "Beregning af prisen på Ivers nye bil: "

A) Beregn arealet af Simons værelse.

B) Hvor mange fisk kan Lotte få for 35 kr?

C) Find omkredsen af cirklen.

D) Undersøg sammenhængen mellem levetid og størrelse.

E) Tegn en rombe med sidelængden 4.

F) Aflæs i diagrammet, hvor mange der kan stå på ski i 4.B.

G) Hvor ofte skal man tage i Tivoli, for at det kan betale sig med årskort?